Référence: https://github.com/jmoore52/SkywalkerRoaster/blob/main/Data/fullrealdataints.txt
En me basant sur les travaux de Josh Moore, qui propose la conception complète d'une interface pour le Skywalker et le logiciel Artisan, je présente une méthode alternative d'utilisation des valeurs de température fournies par la machine.
jmoore52 a extrait une large plage de valeurs numériques de température fournies par un thermistor utilisé comme capteur. Le fichier contenant ces valeurs nous est gracieusement fourni dans son répertoire github.
La machine génère deux courbes de température distinctes. Il semble que l'entreprise ait conçu ces deux courbes pour améliorer la précision des mesures : l'une présente une pente plus raide à faibles températures, tandis que l'autre a une pente plus marquée à des températures plus élevées.
Une pente importante permet d'obtenir une meilleure résolution et précision des mesures. J'ai donc choisi de séparer les courbes pour tirer parti de la précision maximale des données fournies. Ensuite, je présente les équations qui relient la température aux données pour chaque portion de courbe sélectionnée.
Ces équations pourraient être implantées facilement dans le code .ino qui sert à programmer l'interface, essentiellement constituée d'un circuit Arduino.
Based on the work of Josh Moore which outlines the complete design of an interface for Skywalker and the Artisan software, I present an alternative method for utilizing the temperature values provided by the machine.
jmoore52 extracted a wide range of numerical temperature values supplied by a thermistor used as a sensor. The file containing these values is graciously provided to us in its GitHub repository.
The machine provides two separate temperature curves. It seems that the company created these two curves to improve measurement accuracy: one has a steeper slope at low temperatures, while the other has a more pronounced slope at higher temperatures.
A steep slope allows for better resolution and accuracy of the measurements. Therefore, I separate the curves in order to take advantage of the highest precision of the provided data. I then present the equations that relate temperature to the data for the selected portions of the curve.
These equations could be easily implemented in the .ino code used to program the interface, which essentially consists of an Arduino circuit.
The following codes are OCTAVE codes.("Similar to MATLAB")
Using the file "fullrealdataints.txt," we plot the curves of the recorded numerical values as a function of temperature.
Les codes suivants sont des codes OCTAVE. (similaire à MATLAB)
Utilisant le fichier " fullrealdataints.txt" on trace les courbes des valeurs numériques enregistré en fonction de la température.
t(valeurs , valeurs , temps)
close all
clear
t;
ll=length(t);
figure(1)
plot(t(:,3),t(:,2)) % t(:,3) is T , temp value
hold on % t(:,2) is V , numerical value second
colon
plot(t(:,3),t(:,1)) % t(:,1) is V , numerical value first colon
title("Valeurs numériques vs T")
xlabel("T (°F)")
ylabel("Valeurs numériques")
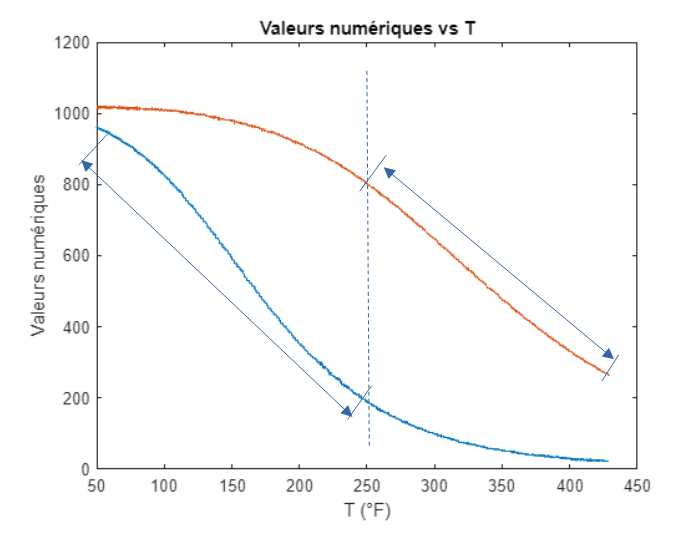
To minimize errors, the curves are used in their segments where the rate of change versus T is more significant.
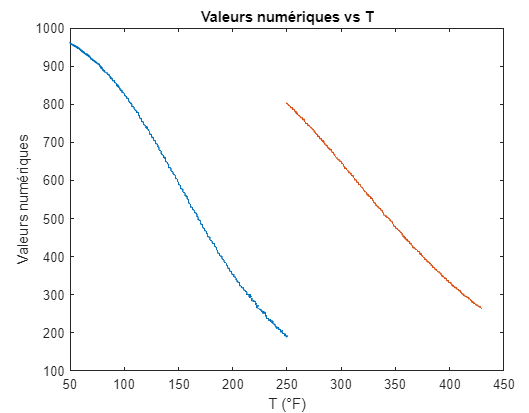
The vector of numerical values is split into two segments at 250°F.
Dans le but de minimiser les erreurs, on utilise les courbes dans leurs portions ou le taux de variation vs T est plus important.
Séparation du vecteur des valeurs numériques en deux portions au niveau de 250 °F.
figure(2)
TB=t(1:1046,3); %Temps low 50 to 250
VB=t(1:1046,2); %numerical value
plot(TB,VB);
hold on
TH=t(1046:1876,3); %Temps high 250 to 450
VH=t(1046:1876,1); %numerical value
plot(TH,VH);
title("Valeurs numériques vs T")
xlabel("T (°F)")
ylabel("Valeurs numériques")
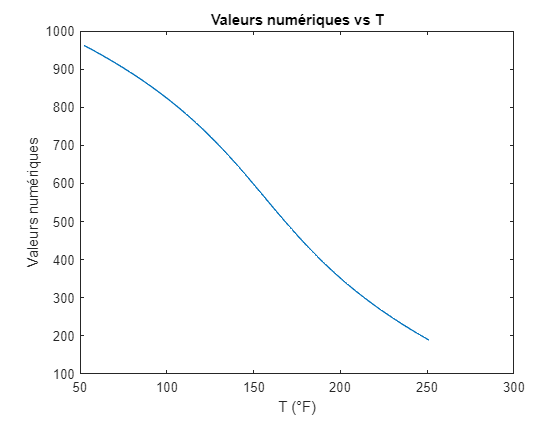
On veut une équation pour calculer T en fonction de V
Pour les températures de 50 à 250 °F, donc pour les vecteurs VB et TB, l'équation polynomial de degrée 3 est:
Linear model Poly3:
f(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 667.5 and std 254.7
Coefficients (with 95% confidence bounds):
p1 = -8.078 (-8.207, -7.95)
p2 = -9.795 (-9.944, -9.647)
p3 = -50.8 (-50.99, -50.6)
p4 = 136.7 (136.5, 136.8)
Goodness of fit:
SSE: 1423
R-square: 0.9996
Adjusted R-square: 0.9996
RMSE: 1.169
p1 = -4.888e-07
p2 = 0.000828
p3 = -0.6513
p4 = 347.9
x=VB;
TBc=p1*x.^3+p2*x.^2+p3*x+p4;
figure(3)
plot(TBc,x)
title("Valeurs numériques vs T")
xlabel("T (°F)")
ylabel("Valeurs numériques")
We want an equation to calculate T as a function of V.
For temperatures ranging from 50 to 250 °F, for the vectors VB and TB, the polynomial equation of degree 3 is:
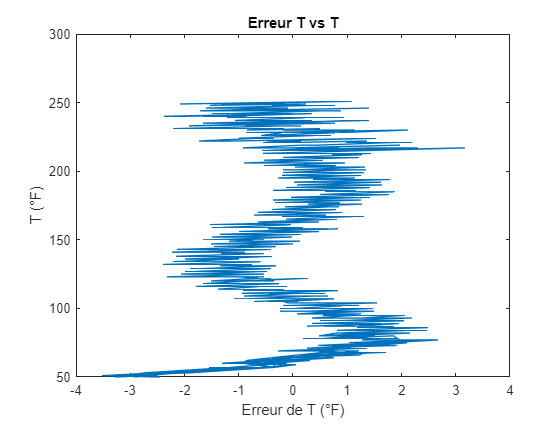
Pour se rassurer que la fonction est précise, on trace la différence entre les valeurs original et la fonction.
dif=TB-TBc;
figure(4)
plot(dif,TB)
title("Erreur T vs T")
xlabel("Erreur de T (°F)")
ylabel("T (°F)")
To ensure the function is accurate, we plot the difference between the original values and the function.
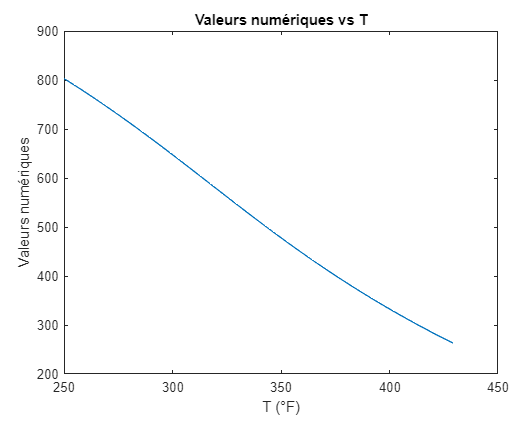
On fait le même cheminement pour la deuxième portion, de 250 à 450.
p1 = -5.054e-07
p2 = 0.0008929
p3 = -0.8165
p4 = 591.4
x=VH;
THc=p1*x.^3+p2*x.^2+p3*x+p4;
figure(5)
plot(THc,x)
title("Valeurs numériques vs T")
xlabel("T (°F)")
ylabel("Valeurs numériques")
We follow the same process for the second portion, from 250 to 450.
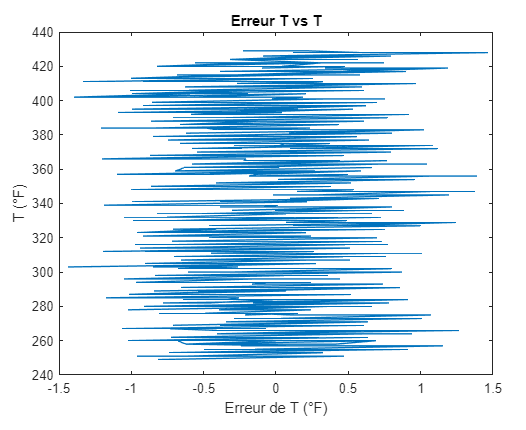
dif=TH-THc;
figure(6)
plot(dif,TH)
title("Erreur T vs T")
xlabel("Erreur de T (°F)")
ylabel("T (°F)")
This site was created with the Nicepage